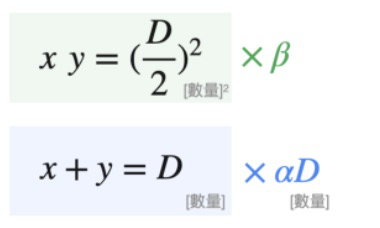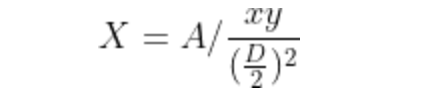W5-1 Curve 协议

计算模型

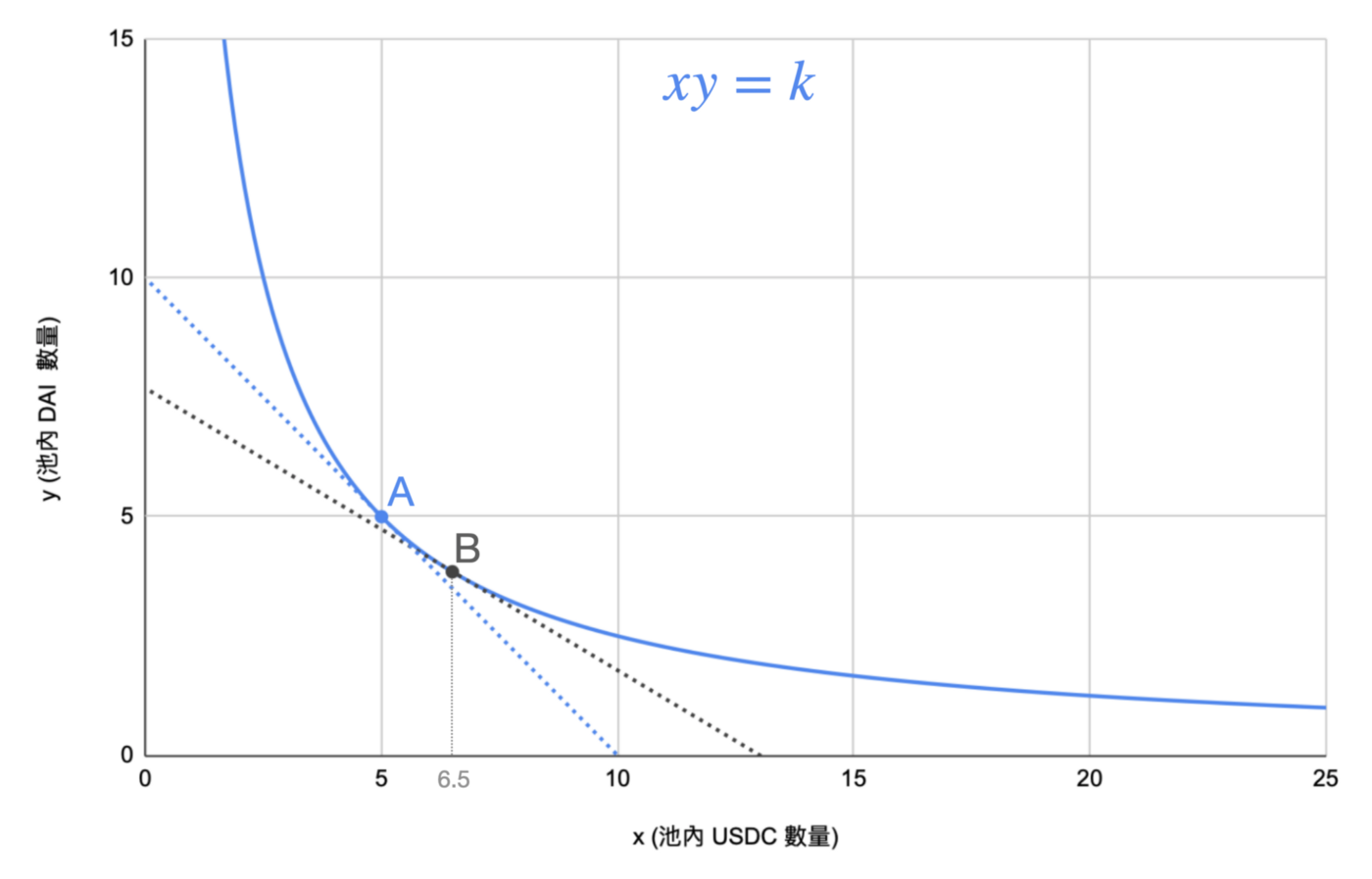
恒定乘积

• 稳定币交易存在的问题
  • 要价格波动⼩（2%以内），⼀次交易的数量需要⼩于池内的1%

常量和模型

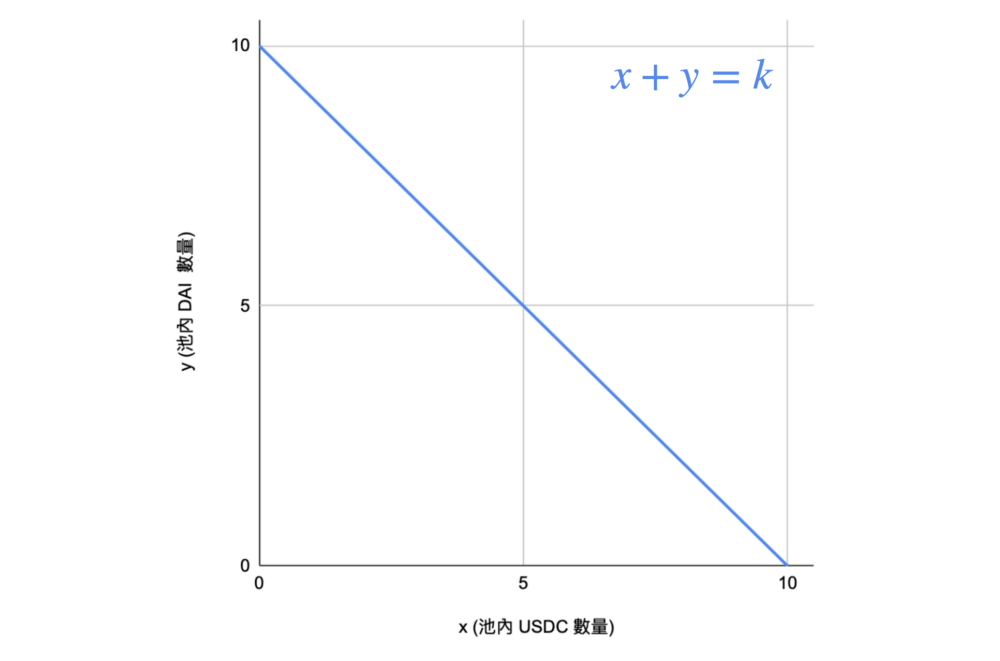
• 公式: \(x + y = k\)

• 优点：永远1:1兑换，没有滑点： \(\Delta X = \Delta Y\)

• 缺点：价格不应供需改变，出现以外部价差时，出现流动性枯竭。

稳定币兑换

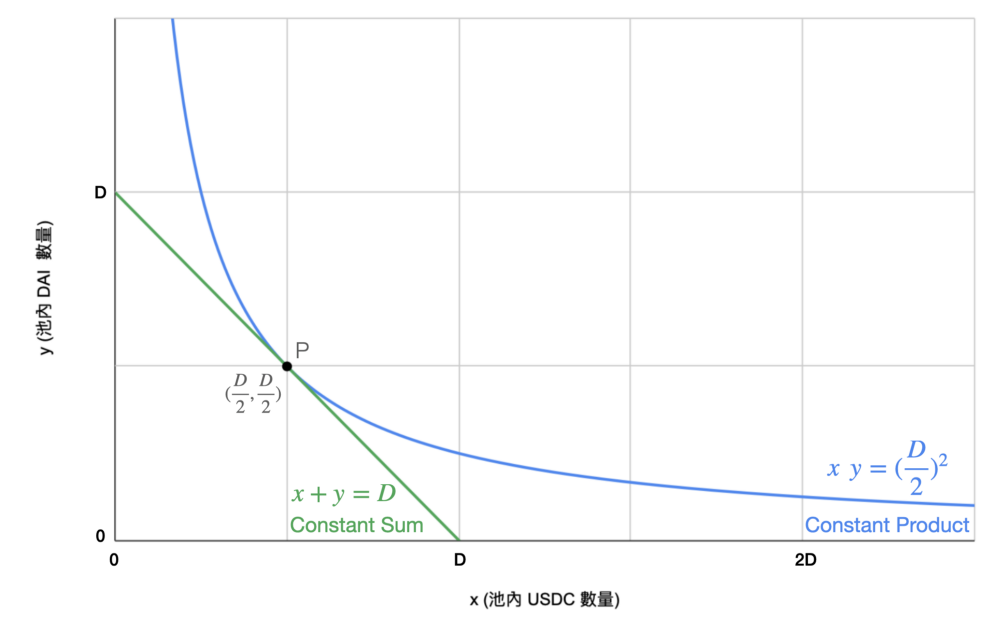
• 恒定乘积：双曲线，两端将接近⽆穷
• 恒定总和: 直线，0 滑点、流动性枯竭

• 理想模型于两者之间，简单⽅式加权平均： \(\alpha D(x+y) + \beta(xy) = \alpha D D + \beta(\frac{D}{2})^2\)

引⼊动态参数

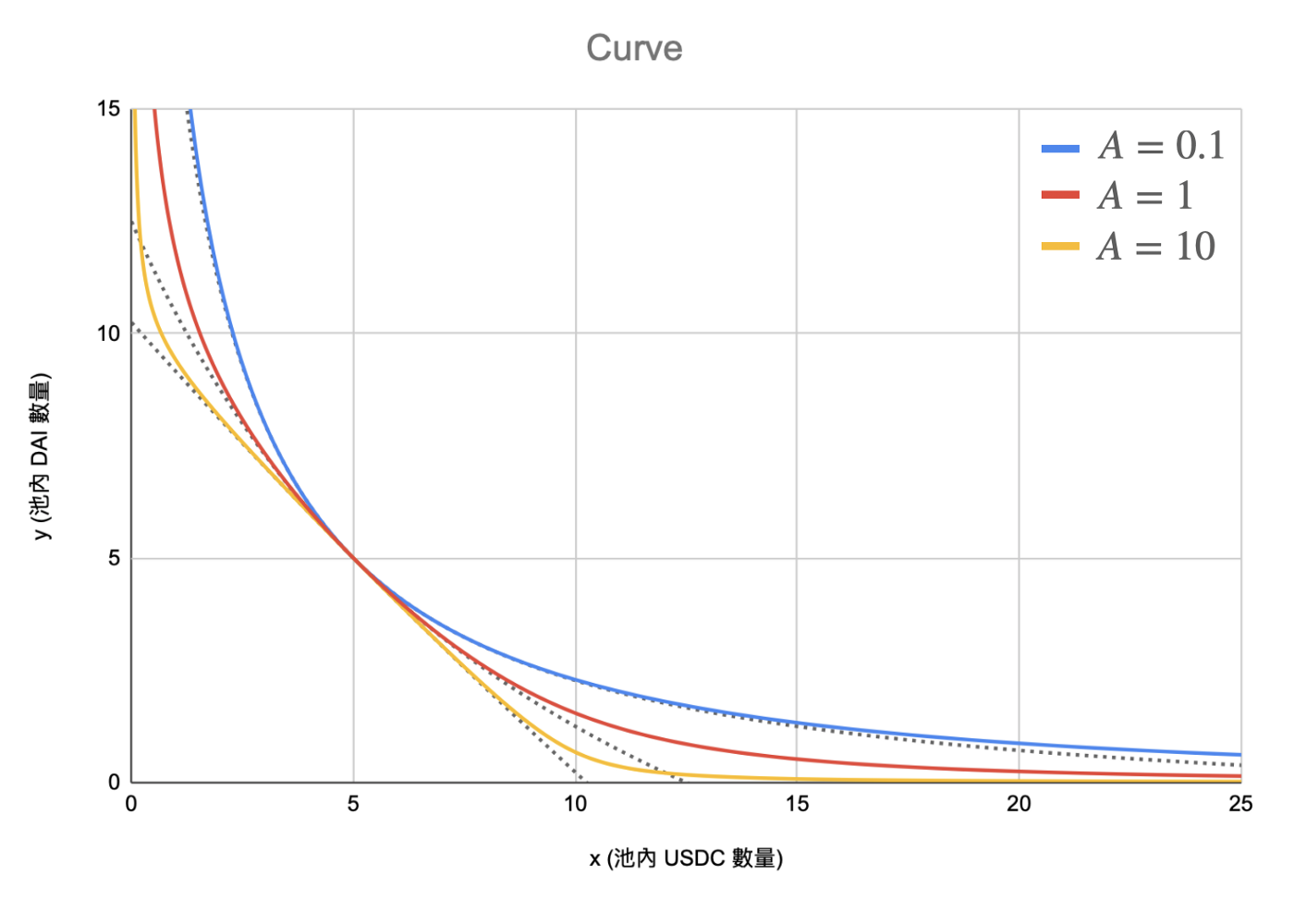
• 模型仍有⼀个缺陷：若希望价格越稳定，则曲线越接近直线，此時会⾯临流动性枯竭问题。能否在靠近平衡点时，χ 越⼤，远离平衡点时越⼩。

• A 为放⼤系数，决定平衡点附件的曲率，A 越⼤滑点越⼩。蓝⾊部分为动态参数，在（0,1）之间：离平衡点越接近時，接近1，接近常量和模型。 离平衡点越远時，接近0，接近常量乘积模型